Recently, I embarked on an informal literature review of the advances in Deep Learning over the past 5 years, and one thing that struck me was the proliferation of activation functions over the past decade. It seems like every large language model (LLM) and fancy neural net architecture making news nowadays uses a slightly different activation function, whereas just a few years ago, the most common practice was to simply use ReLU for the inner layers of a neural network.

Whatever happened to good ‘ol ReLUs, and what compelled the creators of the latest giant large language models (LLMs) to start using different (and fancier) activation functions?

With not a little help from Googling, GPT-4, Claude, and Papers as Code¹, here are my notes on as many activation functions I had the patience to take a look at. Along the way I was able to collect a bit of the history of neural networks along the way, which I’ve provided citations and direct pdf links for. The code for all of the plots in this article can be found in this notebook. Enjoy!

Threshold activation (Perceptron) ²

Rosenblatt building the “perceptron machine” in 1957

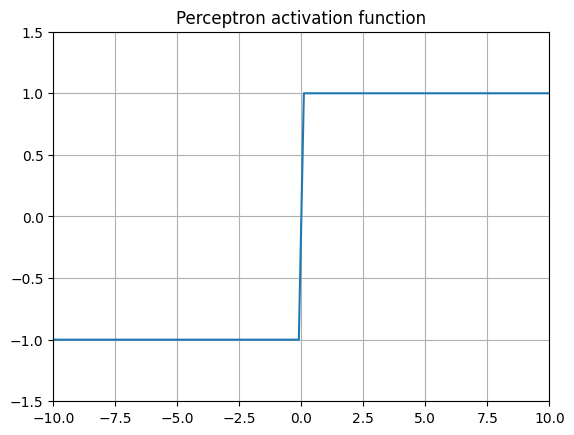
The oldest activation function is the basic perceptron. Conceived at the Department of Psychiatry at the University of Illinois at Chicago by Warren McColloch and Walter Pitts³, it was later more famously physically implemented in hardware by Frank Rosenblatt at the Cornell Aeronautical Laborary in 1957 for the US Navy²⁴. The algorithm is quite simple, consisting of the basic rule that if a value goes above a certain threshold, return 1, else return 0. Some variants return 1 or -1 instead.

Because of its binary nature, the derivative at every point except is 0. This means weights cannot be scaled proprotionally to the labels provided to the network by using a technique like backpropagation.

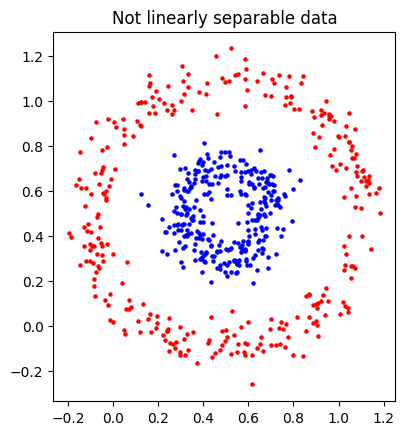
Multilayered perceptrons would reduce to a linear function, making it difficult to non-linearly separable data, like these two donut point clouds.

These limitations led to…

Sigmoid (logistic function) ⁵

The logistic function actually originates from the 1800s, and has been applied for classification problems since the 1940s with the development of logistic regression as a general statistical tool.⁶

Notably, this was the function used in the paper that popularized backpropagation by David Rumelhart, Geoffrey Hinton, and Ronald Williams in 1986.⁵ Interestingly enough, this paper actually caught some flack from none other than Francis Crick (co-discoverer of the structure of DNA) for being biologically implausible ⁷.

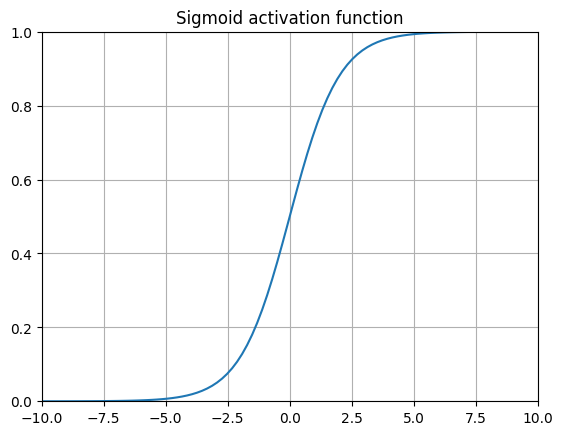
The sigmoid function has several properties that enables it to be effective for classification tasks. First, it’s a smooth differentiable function, which is needed for backpropagation. Second, the function is non-linear. Third, the function squishes values between 0 and 1, enabling us to interpret the output as probabilities. The first two properties are the secret sauce to making multi-layered logistic “neural networks” able to separate non linearly separable data.

There’s a key problem with using sigmoid functions for every single layer of a deep neural network, however. The derivative of the sigmoid gets very small as you get further away from \(x=0\). When backpropagating through many layers, we are essentially taking derivatives of derivatives, thereby making the gradient smaller and smaller as we get away from 0. These leads to the gradient essentially “vanishing”, causing training progress to essentially halt.

Softmax ⁸

The softmax function generalizes the sigmoid for multiple classes, and was popularized by a 1989 paper by John Bridle (although the function itself is much older as it is essentially the probability distribution of the Boltzmann Distribution). When K=2, this function basically reduces to the sigmoid function for the “positive” class.

tanh (Hyperbolic Tangent)

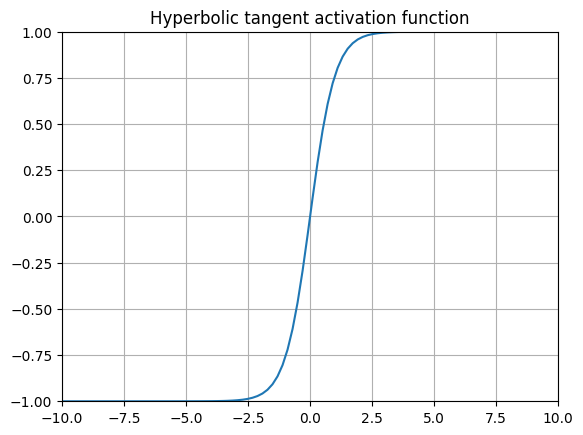
or

or

The original MNIST paper used tanh for every single layer!

The hyperbolic tangent function is a common alternative to the sigmoid, and was most famously used in Yann Lecunn’s 1989 paper on handwritten digit recognition (the original MNIST paper) ⁹. This function is is also well known for being used as the gating function for many variants of Recurrent Neural Networks (RNNs).

Sidenote: Out of sheer curiosity, I did some googling to determine which equation is used by PyTorch under-the-hood since the documentation implies its using the second one. I believe it actually uses glibc via std::tanh under the hood which has some pretty interesting optimizations. The heavily optimized glibc implementation of tanh from 1993 uses four different calculations depending on whether x is really small, less than one, or greater than 22!

Using tanh has the exact same problem as softmax, in that the derivatives further away from \(x=0\) are very small, leading to the vanishing gradient problem.

For many years, the vanishing gradient problem hamstrung progress until the application of…

ReLU (Rectified Linear Unit) ¹⁰

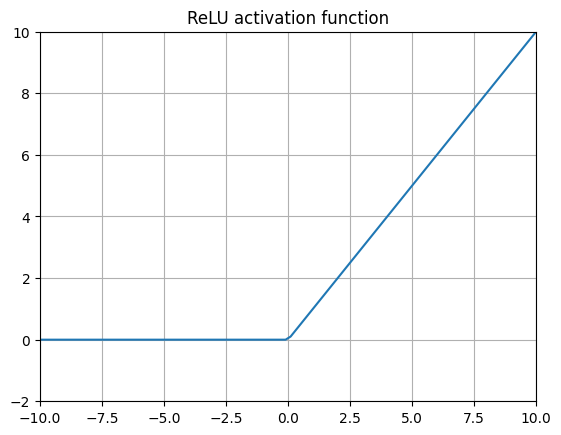
or

The application of RELUs to neural networks in Nair and Hinton (2010) ¹⁰ in some ways kicked off the current revolution in deep learning. By replacing the sigmoids within the inner layers of a neural net with this very simple function, the vanishing gradient problem effectively went away, allowing for the creation of ever deeper layered neural nets.

But how exactly does this work? Aren’t activation functions supposed to be continous and smoothly differentiable to even work? ReLUs are not even differentiable at \(x=0\)! In practice this is not a big deal and the computational efficiency gains of using ReLUs are well worth it. The gradient for ReLU is simply 0 for values less than 0, 1 for values greater than 0, and most libraries simply arbitrarily set the gradient at \(x=0\) to 0. This makes ReLU by far the most computationally efficient activation layer, requiring no exponentiation whatsoever, which can slow down compute significantly. ReLUs work just fine for many, many complex machine learning tasks and were used for the inner layers of just about all deep neural nets (including AlphaGo ¹¹), prior to 2016.

However, the representational capacity of ReLUs can be limiting for performance, namely because all negative values are simply clamped to 0. This leads us to…

Leaky ReLU (Leaky Rectified Linear Unit) ¹²

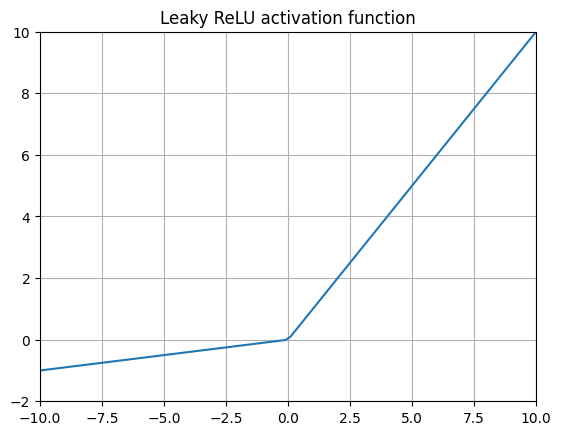
or

Also known as LReLU and sometimes PReLU (for parameterized ReLU)¹³ to highlight the fact that the alpha parameter for the negative value slope can be manually tweaked.

This layer addresses one downside of ReLU by simply allowing negative input values to propagate to the next layer by some constant. Leaky ReLU is an attempt to get better performance by using a small slope for negative values instead, but the choice of this slope can be rather arbitrary in practice.

The choice of using a negative slope means that highly negative values keep getting more and more negative, leading us to…

ELU (Exponential Linear Unit) ¹³

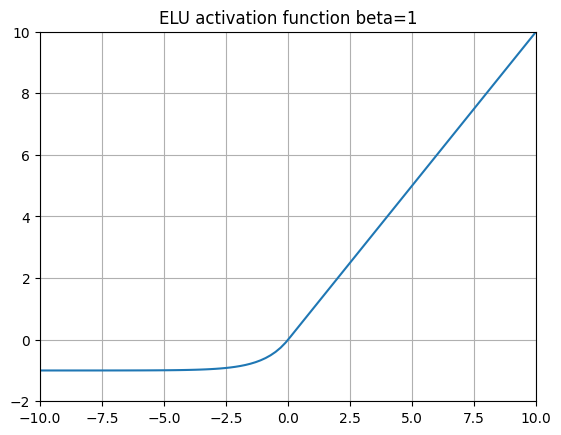
ELUs take the idea of LeakyReLUs and replaces the negative slope with an exponentiation function \( \alpha (e^x - 1) \). This means that is \(x\) gets more and more negative, \(y\) will converge to \(-\alpha\).

In 2015, the authors of the ELU paper demonstrated excellent performance on ImageNet when swapping out ReLUs with ELU activation functions.

GELU (Gaussian Error Linear Unit) ¹⁴

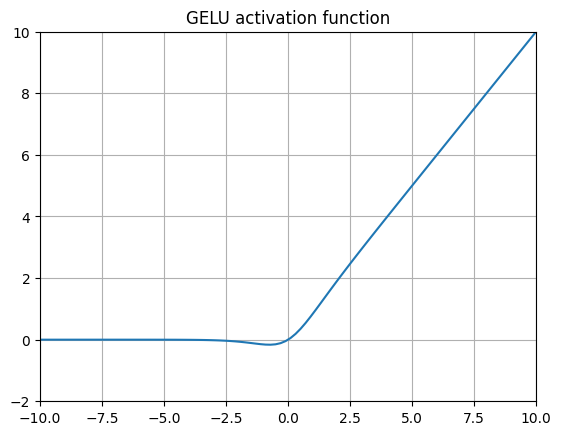
Where \(\Phi(x)\) is the standard Gaussian cumulative distribution function (CDF).

so long as \(x\) is drawn from a normal distribution with a mean of 0 and standard deviation of 1.

Very often approximated with “QuickGELU”. For example, in the source code for CLIP.¹⁵

Introduced in 2016, GELUs (and SiLUs which appeared in the same paper) are probably the most archetypal non-ReLU activation function today. The core idea is that in cases where we expect the inputs of a layer to be normally distributed (when using batchnorm, for example), the CDF of a given input variable \(x\) represents the probability of that input being less than or equal to the observed input. So \(x * \Phi(x)\) simply scales the input \(x\) by its probability of occurence assuming its normally distributed.

Looking at the shape of the function itself, it’s interesting to compare the representational capacity of this function (similar to SiLU, Swish, and SoLU) to Leaky ReLU and ELU. Here we let some negative values through, but as \(x\) gets very negative, the values gradually get clamped to 0 whereas with Leaky ReLUs they would instead simply get smaller and smaller and with ELUs they would converge to \(-\alpha\). GELUs avoid the vanishing gradient problem while still letting some negative values through.

GELU is used in GPT-3¹⁴, BERT¹⁶, and in the original CLIP¹⁵ paper along with a whole series of models at OpenAI. In practice, due to the common usage of the QuickGELU approximation, GeLU is effectively very similar to SiLU/Swish-1 with the sole difference being a scaling of the x input to the sigmoid function.

SiLU (Sigmoid Weighted Linear Unit) ¹⁷

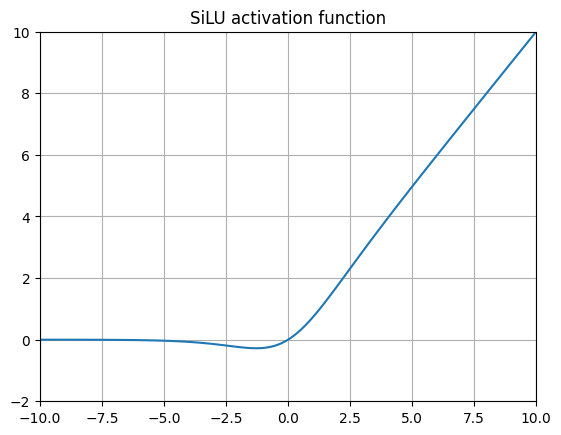
SiLUs were introduced in the original GELU paper from 2016 and later expanded upon by other researchers. When we replace the Gaussian CDF with the Logistic CDF (which is basically the sigmoid function), we wind up with this function. Subsequent researchers ran benchmarks of SiLU for playing Atari Games using Reinforcement Learning and found a great improvement.

Swish ¹⁸

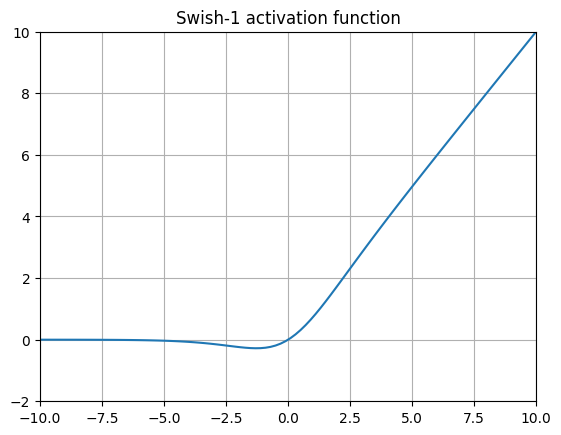
It’s shaped like the Nike logo, get it? Swish is bascially a slight modification of SiLU via the addition of a trainable \(\beta\) parameter, which effectively adds another gradient term. Many, many implementations of this omit the beta parameter altogether (typically called Swish-1), making this activation function identical to SiLU!

SoLU (Softmax Linear Unit) ¹⁹

Seeing a pattern here? This simply replaces the sigmoid in SiLU with a softmax function. The main idea here is to aim interpret the outputs of a neuron. This would seem to significantly increase the number of exponentiations that need to be computed and the size of the layer output. The authors report models become handicapped to performing about the level of equivalent models with 30-50% as many params. To get around this issue, the authors claim that wrapping each SoLU with a LayerNorm effectively resolves this issue, giving a reasonable tradeoff between performance and model interpretability.

GLU (Gated Linear Unit) ¹⁷

GLUs represent an outgrowth of some ideas from RNNs - namely to use learnable gates to control the information that flows into subsequent layers, discarding information if necessary. GLUs originate from a (pre-transformer) 2016 paper which aimed to develop gated convolutional networks (GCNs) for language modeling.¹⁷

The basic idea from the original paper is to do a linear transformation of \(x\) with a weight matrix V and bias c \((xV +c)\). Then apply a gating function \(sigmoid(xW + b)\), effectively deciding what goes into the next layer or not in an operation inspired by RNN gating.

One notable very recent application of GLUs is in the Evo “Striped Hyena” model for long genome sequence scale modeling.²⁰

Although the idea of using convolution for language modeling has fallen by the wayside since 2016, the GLU activation layers from this paper live on in slightly modified form today…

GEGLU and SwiGLU ²¹

This GeGLU and SwiGLU were developed as variants of GLU in a 5-page single author paper by Noam Shazeer from 2020.²¹ The basic idea is to simply combine GLU with GELU or Swift, replacing the sigmoid gate with either a GELU gate or a Swish gate.

The original paper provides absolutely no rationale for why this approach leads to better performance metrics, simply attributing it to “divine benevolence”, although thinking about the shape of the activations, I would venture to guess the performance might have something to do with the lack of upper bound created by the using a \(sigmoid(x) \) in Swish and GELU.

SwiGLU has since been adopted in a number of prominent LLMs including Google’s PaLM ²² and Meta’s Llama2 ²³, making this techniques just about the state-of-the-art in language modeling right now!

Smooth SwiGLU

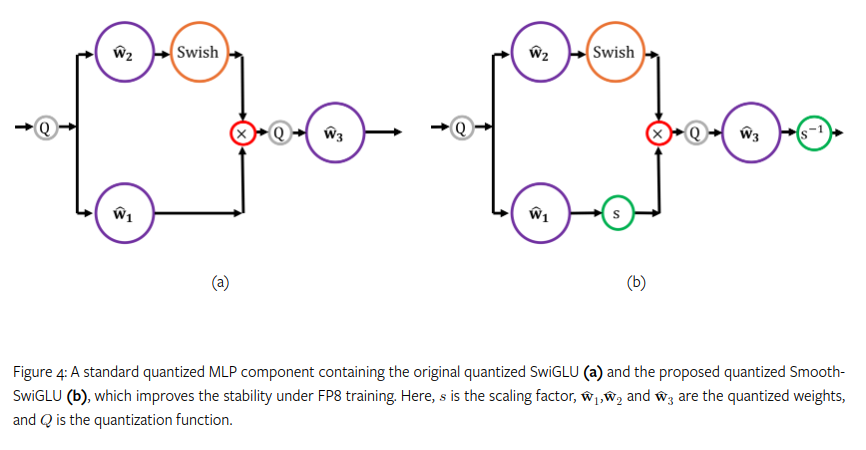
In September 2024, Intel’s Habana labs found critical instabilities in training an FP8 large language model on 2 trillion tokens that was ultimately traced to usage of SwiGLU. After hitting 200 Billion tokens, they found that outliers would tend to be amplified. To address this issue they developed a new activation function called Smooth-SwiGLU. ²⁴

Conclusion

One takeaway that became evident when reviewing these functions and their histories was that despite the intimidating number of acronyms out in the wild now, many of the commonly used activation functions post-2016 essentially use the same “Swish” shape and \(x * F_{cdf}(x)\) function. SiLU, Swish, GeLU, and SoLU fall under that umbrella.

These approaches can cost quite a bit more compute than RELU. For example, the FlashAttention-3 paper points out that a H100 SXM5 GPU has 989 TFLOPs of F16 matmul but only 3.9 TFLOPs for special functions like the exponential used for sigmoid and softmax calculations. ²⁵ To really squeeze out performance from hardware requires fancy asynchronous scheduling to make deep learning go Brr. ²⁶

What is evident, however is how heavily invested different groups are in squeezing every last bit of performance out of LLMs, with the last set of activation functions I mention here (SwiGLU and GEGLU) quite computationally demanding.

Note: There were a lot more activation functions I researched but did not write about, including CELU, RELU2, RELU6, PReLU, SELU, Softplus, and MISH. If I’ve omitted any important ones, please let me know!

Citations

BibTeX Citation

@article{
    du2024alltheactivations,
    author={Lawrence Du},
    title={All The Activations (and a history of deep learning)},
    year={2024},
    url={https://dublog.net/blog/all-the-activations/},
}